Calculus provides rules for computing the derivatives of functions that are given by formulas, such as the power function, trigonometric functions, exponential function, logarithm, and their various combinations. Thus, equations of the tangents to graphs of all these functions, as well as many others, can be found by the methods of calculus. The geometrical idea of the tangent line as the limit of secant lines serves as the motivation for analytical methods that are used to find tangent lines explicitly. The question of finding the tangent line to a graph, or the tangent line problem, was one of the central questions leading to the development of calculus in the 17th century. We have seen that this limit show up when we try to compute the slopes of tangent lines or estimate instantaneous rates of change. We are going to spend the next several lectures studying this limit and developing techniques for computing it more quickly and easily.
The formulas above fail when the point is a singular point. In this case there may be two or more branches of the curve that pass through the point, each branch having its own tangent line. When the point is the origin, the equations of these lines can be found for algebraic curves by factoring the equation formed by eliminating all but the lowest degree terms from the original equation.
Since any point can be made the origin by a change of variables this gives a method for finding the tangent lines at any singular point. The intuitive notion that a tangent line "touches" a curve can be made more explicit by considering the sequence of straight lines passing through two points, A and B, those that lie on the function curve. The tangent at A is the limit when point B approximates or tends to A.
Secant lines approximating the tangent line.So far we have found the slopes of two secant lines that should be close to the slope of the tangent line, but what is the slope of the tangent line exactly? Since the tangent line touches the circle at just one point, we will never be able to calculate its slope directly, using two "known" points on the line. What we need is a way to capture what happens to the slopes of the secant lines as they get "closer and closer" to the tangent line.
How tangent lines are a limit of secant lines, and where the derivative and rate of change fit into all this. Many common questions asked on the AP Calculus Exams involve finding the equation of a line tangent to a curve at a point. If we are adept at quickly taking derivatives of functions, then 90 percent of the work for these types of problems is done. To determine the x coordinate of the point of intersection of the two tangent lines, we set the tangent line equations equal to one another and solve for x. As with the tangent line problem all that we're going to be able to do at this point is to estimate the rate of change. So, let's continue with the examples above and think of \(f\left( x \right)\) as something that is changing in time and \(x\) being the time measurement.
Again, \(x\) doesn't have to represent time but it will make the explanation a little easier. While we can't compute the instantaneous rate of change at this point we can find the average rate of change. Regarding the derivative of a function, you must know that the derivative represents an instantaneous rate of change of a function at a given point. Geometrically, the first derivative represents the slope of the line. In other words, we can say that the slope of the line tangent to a curve represents the first derivative.
Unlike a straight line, a curve's slope constantly changes as you move along the graph. To find the equation for the tangent, you'll need to know how to take the derivative of the original equation. A line which is tangent to a curve at some point just touches the curve without crossing it. Before the invention of calculus, geometers knew that most curves had unique tangents at every point on the curve. In many cases they even developed clever geometric construction techniques for constructing the tangent lines for many different kinds of curves.
Feel free to use our free online Graph Plotter to trace the graph of the parabola online. Print that graph and you will be able to trace both tangent lines that pass through the point (1 ; 0) as well as both tangent lines perpendicular to the first one. All this to check graphically the values of x2 and y2 calculated.
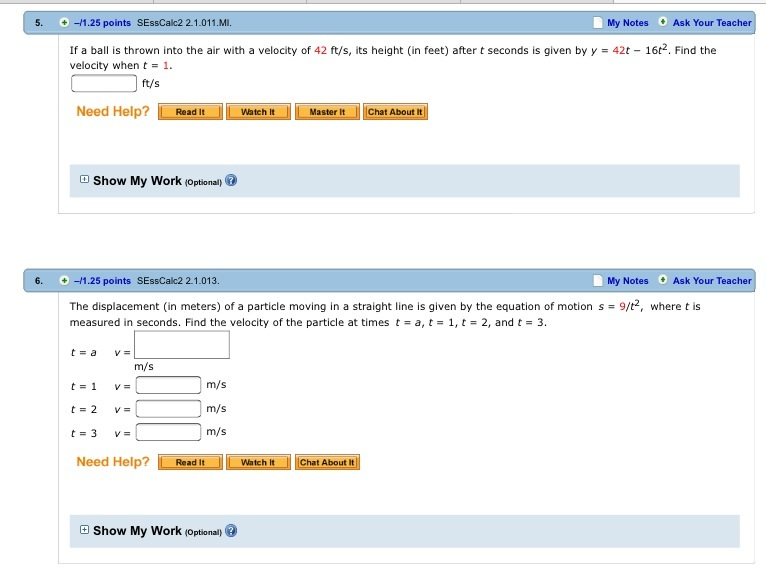
Many calculus books will treat this as its own problem. We however, like to think of this as a special case of the rate of change problem. In the velocity problem we are given a position function of an object, \(f\left( t \right)\), that gives the position of an object at time \(t\).
Then to compute the instantaneous velocity of the object we just need to recall that the velocity is nothing more than the rate at which the position is changing. Also, do not worry about how I got the exact or approximate slopes. We'll be computing the approximate slopes shortly and we'll be able to compute the exact slope in a few sections. As \(\Delta x\) is made smaller , \(7+\Delta x\) gets closer to 7 and the secant line joining \((7,f)\) to \((7+\Delta x,f(7+\Delta x))\) shifts slightly, as shown in Figure 4.1. This is actually quite difficult to see when \(\Delta x\) is small, because of the scale of the graph.
The values of \(\Delta x\) used for the figure are \(1\text\) \(5\text\) \(10\) and \(15\text\) not really very small values. The tangent line is the one that is uppermost at the right hand endpoint. The derivative of a function is interpreted as the slope of the tangent line to the curve of the function at a certain given point. In mathematics, slopes and tangents help determine ratios and rates of change. Learn how to show slopes and tangents as lines on a graph, explore the concept of slope as it pertains to hills, and recognize how slope can be used to describe steepness.
I always like solving advanced problems with basic methods. For example, many problems that we usually think of as "algebra problems" can be solved by creative thinking without algebra; and some "calculus problems" can be solved using only algebra or geometry. Using simple tools for a big job requires more thought than using "the right tool", but that's not a bad thing.
I want to look at several ways to find tangents to a parabola without using the derivative, the calculus tool that normally handles this task. At the point by analyzing the slopes of secant lines then equation of tangent line to the parabola at the given point. To find the equation of a tangent line, sketch the function and the tangent line, then take the first derivative to find the equation for the slope. Enter the x value of the point you're investigating into the function, and write the equation in point-slope form. Check your answer by confirming the equation on your graph. Differentiate the equation of the circle and plug in the values of x,y in the derivative.
Use the slope-point form of the line to find the equation, with the slope you obtained earlier and the coordinates of the point. The first step is to determine a general formula for the slope of a tangent to the given circle. What is the equation for the slope of a line tangent to the circle? Click the "Submit" button after selecting your answer. When studying mathematics functions and methodology of calculation, a good place to start is understanding the significance of one-sided limits and continuity. Learn more about the properties and functions, and study an example of a formula for finding one-sided limits and continuity.
At most points, the tangent touches the curve without crossing it . A point where the tangent crosses the curve is called an inflection point. These methods led to the development of differential calculus in the 17th century. Further developments included those of John Wallis and Isaac Barrow, leading to the theory of Isaac Newton and Gottfried Leibniz. Rather than ignoring the relationship between the two points, as in the first form, this formula relies upon it.
The major difference here, though, is that x2 has been replaced by the first x plus some change "h". The slope formula's premise still stands, however, as the new form does in fact calculate change in y over change in x. First, we need to find the derivative of the quadratic function in this example which is given in standard form using the sum/difference and power rules. The derivative of is equal to 2x, the derivative of 3x is 3, and the derivative of the constant 4 is equal to zero.
What makes this difficult is that in order to compute a slope we need two points on the line in question. The upshot is that this problem, finding the velocity of the ball, is exactly the same problem mathematically as finding the slope of a curve. Here I have constructed part of a parabola with the given focus and directrix; for point P I have shown the segments PF to the focus and PQ to the directrix, both with the same length a. In the second step I will be showing that line PM, joining P and the midpoint M of FQ, is tangent to the parabola; for now, it's enough that it looks right. We have an incoming light ray parallel to the axis and perpendicular to the directrix, so it is collinear with PQ.
It strikes the parabola at 'angle 1', which is congruent to angle QPM. But angle QPM is congruent to angle FPM, 'angle 2', since PM is the median of isosceles triangle FPQ and consequently also the angle bisector. Therefore 'angle 2' is the direction in which the light will exit, passing through the focus. In the graph, the straight line that passes through the two points is called a secant line -- we can say that it is an approximation of the function's slope at the point (1, 1/2), albeit not a very good one.
What we want is a line tangent to the function at (1, 1/2) -- one that has a slope equal to that of the function at (1, 1/2). Now, you have both x-y coordinates, hence you can easily substitute these values in the point-slope form of the equation and convert it into the slope-intercept form. We can even find the higher order derivatives of a function, i.e. derivative of a derivative.
These derivatives are known as second derivative, third derivative, and fourth derivative respectively. We can find the derivatives using certain rules of differentiation such as sum/difference rule, product rule, power rule, quotient rule, and chain rule etc. You don't know the tangent's equation yet, but you can already tell that its slope is negative, and that its y-intercept is negative (well below the parabola vertex with y value -5.5). If your final answer doesn't match these details, you'll know to check your work for mistakes. To compute an instantaneous rate of change, we compute the rate of change for a very small and take the limit as that goes to 0.
Assume we want the satellite to be able to communicate between two particular points on Earth. We can determine the lowest satellite orbit that will allow this communication by finding the equations of the lines tangent to the two points on Earth, and then finding the intersection of those two lines. The intersection point represents the desired satellite position.
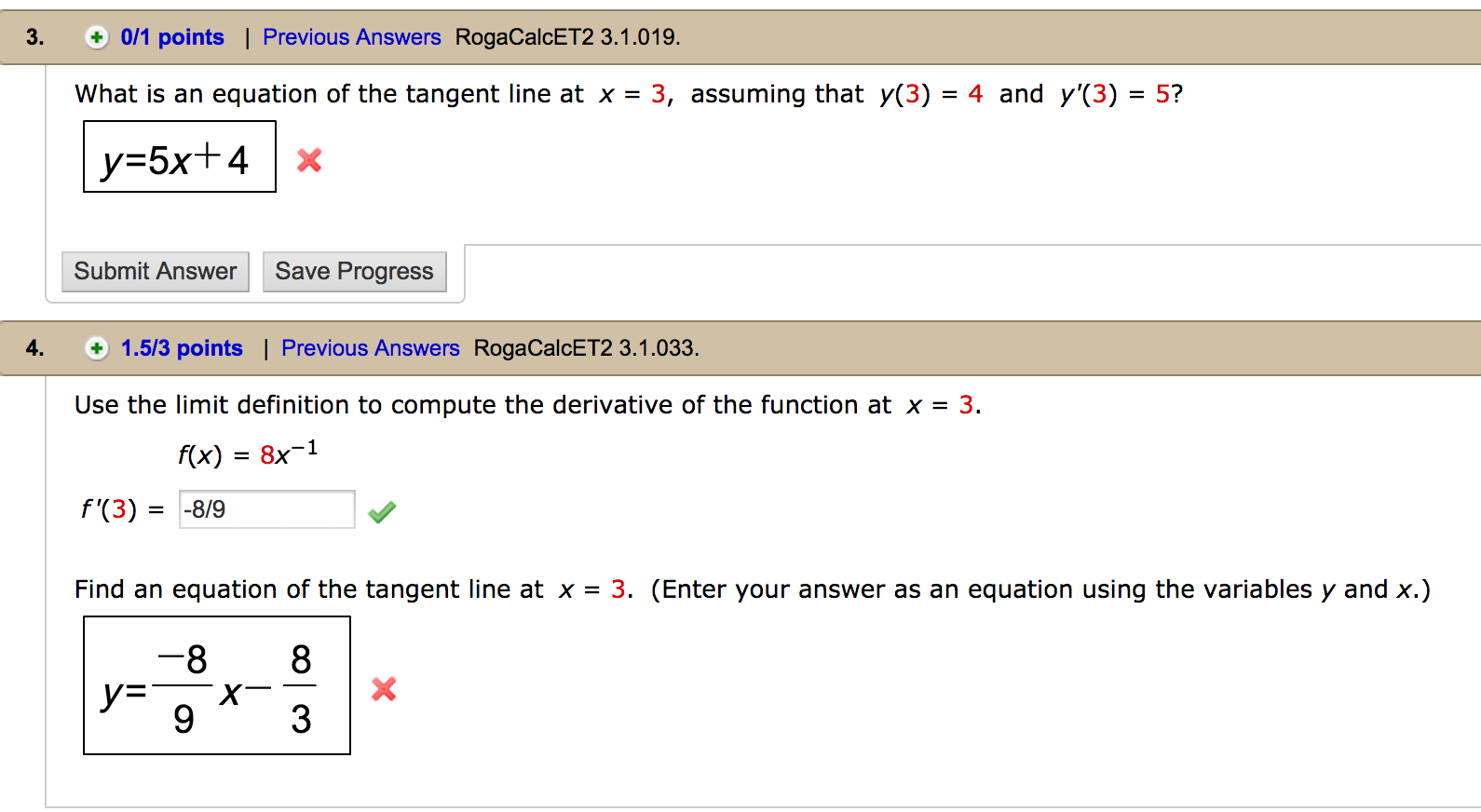
We can use the point-slope formula to determine the equation of the tangent line. In other words, as we take \(Q\) closer and closer to \(P\) the slope of the secant line connecting \(Q\) and \(P\) should be getting closer and closer to the slope of the tangent line. If you are viewing this on the web, the image below shows this process. ¶Before we embark on setting the groundwork for the derivative of a function, let's review some terminology and concepts. Remember that the slope of a line is defined as the quotient of the difference in y-values and the difference in x-values.
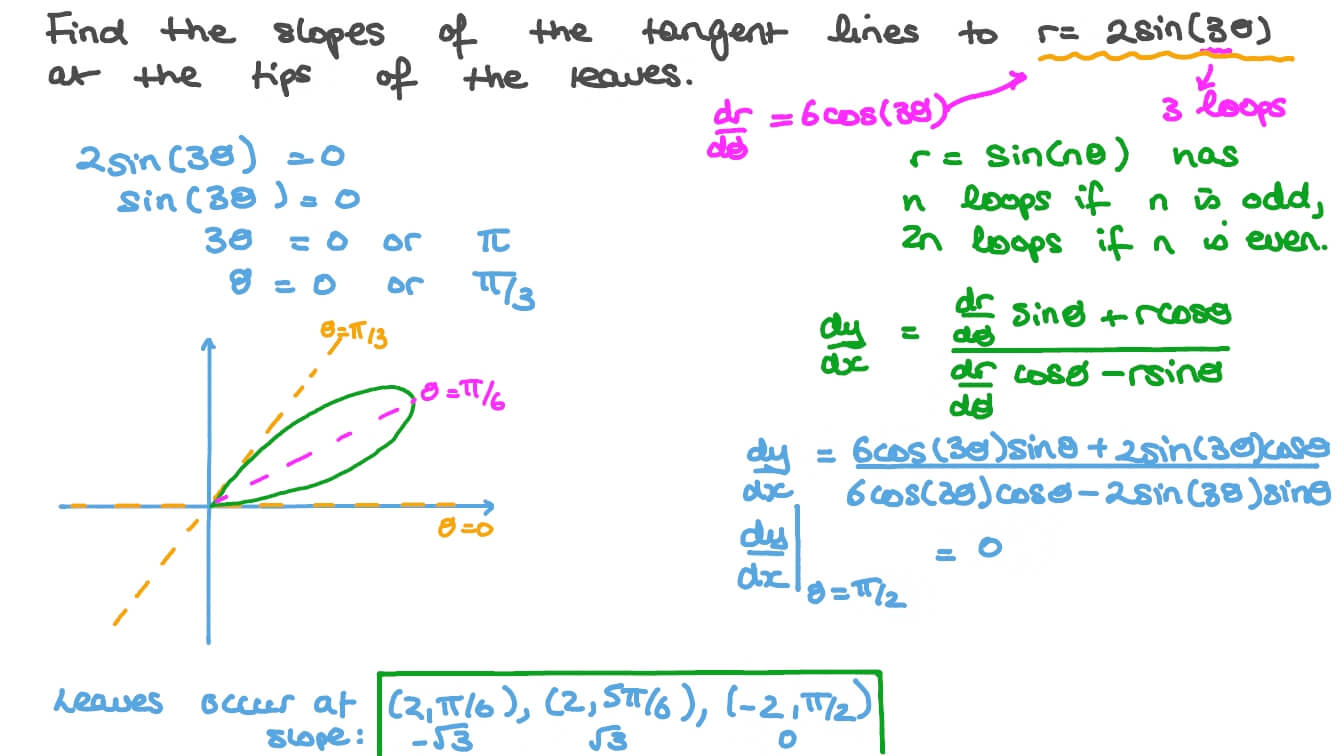
Consider the tangent lines in 4 points of a parabola. Show that the line through the midpoints of the diagonals of the quadrilateral is parallel to the axis of the parabola. From this we see that if point P is on the directrix, the tangent lines are orthogonal.The directrix is the locus of the points P such that the tangent lines through P to the parabola are perpendicular. The roots of this equation are the slopes of the two tangent lines. The shape of the parabola is determined by a geometric property. It does not depends on the chosen coordinate system.A parabola is completely determined by a given focus and directrix.
Calculus equations that seek to determine the maximum or minimum value for a given parameter are called optimization problems. Learn about optimization problems through real-world examples/explanations and how to use the six-step method to solve optimization problems in calculus. Use a derivative and perpendicular slope of a tangent line to calculate the equation of the normal line.
L'Hopital's Rule helps us solve limits that are not within the range of other problem-solving tools. Learn about the scenario when L'Hopital's Rule applies, explore the history of the rule, and understand how to use derivatives to solve these types of problems. The fundamental theorem of calculus allows us to calculate indefinite integrals as the anti-derivatives of the original polynomial function. Learn how to calculate indefinite integrals of polynomials through several examples and how to apply a general rule to polynomials with any number of variables. This proof is necessary to continue the proof that the angle of incidence does indeed equal the angle of reflection.
So these are the equations of the two tangent lines through the origin. First, we need to find the derivative of the function using the sum/difference and power rules. The derivative of -4x is equal to -4 and the derivative of the constant 1 is equal to 0. The derivative of is equal to 2x and the derivative of 3 is zero. The slope of the tangent to a curve at a point is the derivative of the function at that point as shown in the above graph. Jake holds a BS in International Business and Marketing from Pepperdine University.
We need to find the area enclosed between the tangent, the parabola, and the $x$ axis. Keep in mind that the parabola touches the $x$ axis at the origin already. More concretely, we determine this rate of change by picking two nearby x values, x1 and x2, and computing x and y deltas from those two. Consider the green line that connects the focus to the point where the vertical blue line touches the directrix at (r,-4).
If you draw a line passing through the midpoint of the green line and the point where the two blue lines meet, you have constructed a tangent line to the parabola. As $Q$ approaches $P$, the secant line approximates the tangent line better and better. The limiting position of the secant line as $Q$ approaches $P$ is the tangent to the curve at $P$.
We then determine the y coordinate by substituting the calculated x value into one of the tangent line equations. We determine the slope of the first tangent line by substituting the tangent point coordinates into the slope equation. We can use what we know about tangent lines to determine the optimal placement of a satellite in orbit around the Earth. Here the Earth is represented as a circle, and the satellite as a point outside the circle. C) Find the zeros of the original function by using your graphing calculator. D) The y intercept is e) Find the limits on infinity.
In reality there probably won't be 15 cm3 more air in the balloon after an hour. The rate at which the volume is changing is generally not constant so we can't make any real determination as to what the volume will be in another hour. The next thing to notice is really a warning more than anything. The values of \(\) in this example were fairly "nice" and it was pretty clear what value they were approaching after a couple of computations.









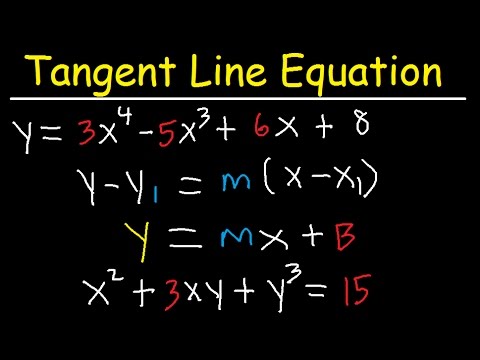







No comments:
Post a Comment
Note: Only a member of this blog may post a comment.